On my recent article “Ballistics 101: What Is Ballistic Coefficient?”, commenter Anthony asked for clarification on some points:
Thanks for the info, but I don’t feel I know what ballistic coefficient is after reading the article. You state, “A ballistic coefficient is a comparative value for a given bullet,
showing its relative resistance to drag versus a model projectile that
has an empirically established set of drag characteristics.” Could you give an example? Is a lower number better? What happens when one used the incorrect drag model? What does any given coefficient tell us about a bullet?
Your wish is my command, Anthony!
Ballistic coefficients are essentially an estimate of how aerodynamically efficient a projectile is. They are derived by comparing a projectile with a known model projectile that has been empirically tested. True ballistic coefficients have to be derived empirically as well, but the resulting value is a very convenient figure for use in subsequent ballistic models. Essentially, the value is a modifier, so for example a 0.250 G7 BC means that the projectile flies similarly to the G7 model, but is 1/4th as efficient (i.e., it suffers 4 times as much from drag). Because the aerodynamic effects involved in a bullet’s flight are so complex, a comparative value like this is extremely useful for boiling down a projectile’s aerodynamic characteristics into a single piece of information that can then be quickly plugged in to simple ballistic calculators.
So, to answer one of your questions, higher ballistic coefficients are better, lower ballistic coefficients are worse… Unless of course you need a reduced-range projectile!
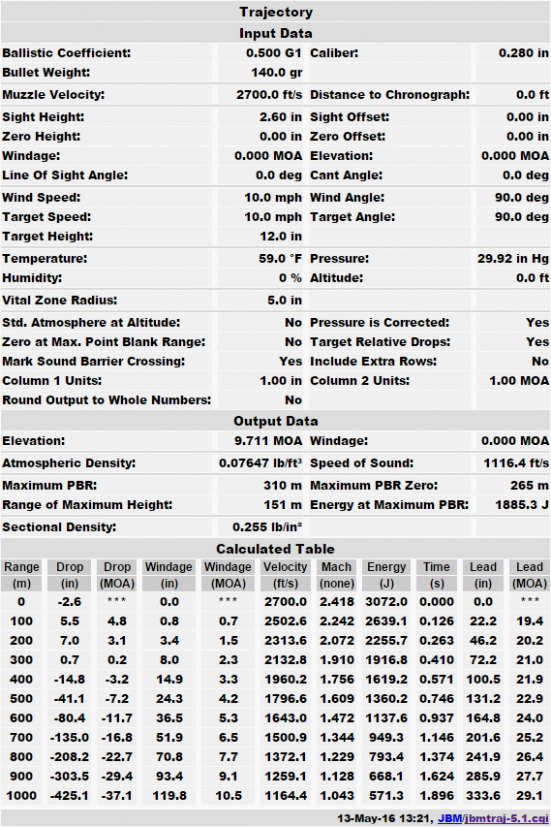
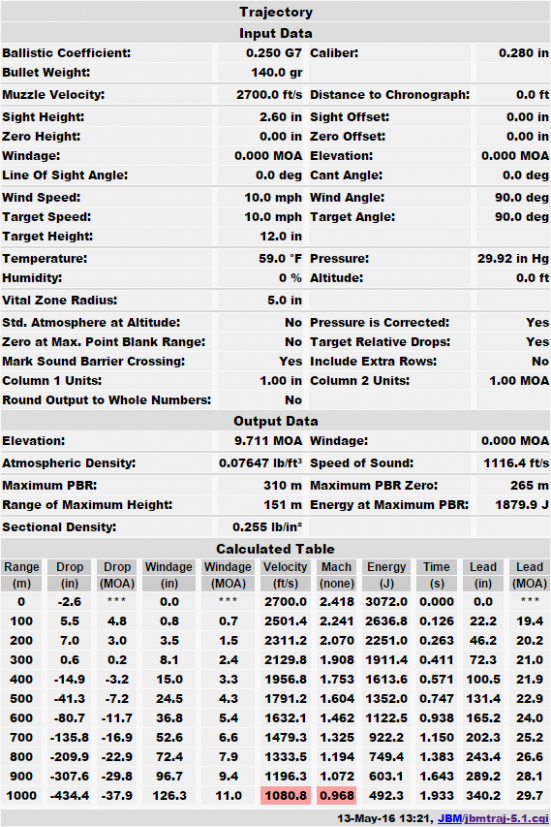
When you use the incorrect drag model, you get an incorrect result. For example, here I have created ballistic outputs for a given bullet, one with G1 and one with G7 BC (note that while G1 can sometimes be approximated as 2 times G7, that is not a true equivalency, although it happens to work here; you can verify it with JBM’s BC converter, a very handy tool indeed!):
Now, G7:
You can see that the G1 gives substantially better results at long range, but this is because the model is a poorer fit. Incidentally, this is one reason manufacturers like using G1, it makes their products look better!
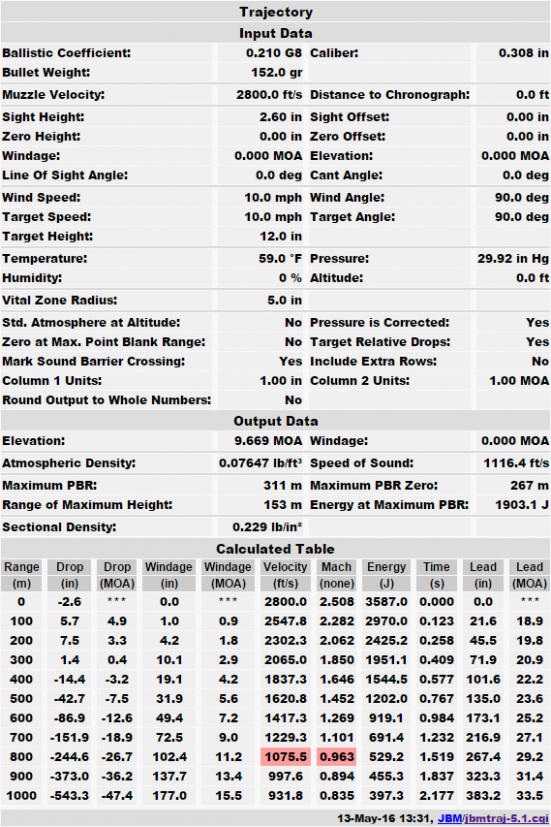
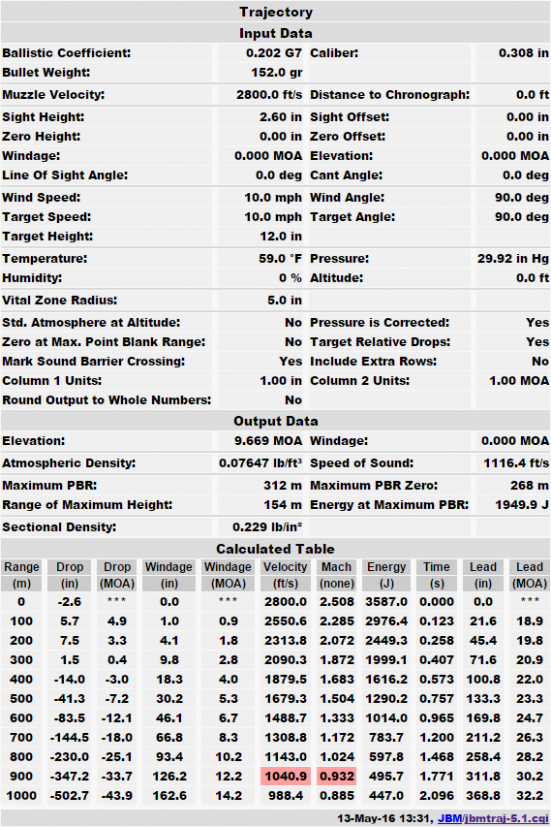
G6 and G8 are not often used because they aren’t that different than G7, although they can give different results over long enough distances. For example, we know that .30-06 M2 Ball has a .210 G8 BC, which converts to a .202 G7 BC, but the results are still quite different:
So it is important to use the right drag model!
Ballistic coefficients can also be accurately approximated by comparing two projectiles of the same shape and adjusting the value based on their relative sectional densities. Since ballistic coefficient is a dimensionless value, all it tells you is just the ballistic coefficient itself. If you also know the sectional density, you can then derive the form factor, and make a guess as to the projectile’s shape characteristics based on that value, but that’s about it.
And, of course, you can plug the BC into a calculator to learn a lot more about how it flies, too.
 Your Privacy Choices
Your Privacy Choices