This post is part of a short series I’m calling simplistic ballistics. My goal is to illustrate some basic rules of shooting without the math heavy charts and formulas. I’m looking to lay out in clear language a core rule, and also give you an understanding on why a bullet behaves the way it does. I would caution experienced engineers and dedicated precision shooters: you should already know this, and what I’m writing here is both simplified and straightforward.

Today we’re talking about shooting on an incline. When I was in retail, I sold a lot of laser rangefinders to a lot of hunters, and had regular debates about changes to a bullet’s flight path on angles. When you’re next to the Rocky Mountains, that conversation comes up a lot, and you’d be surprised how many people are unfamiliar with this core concept:

When shooting uphill or downhill, a bullet experiences less drop than a similar shot fired on a flat plain.

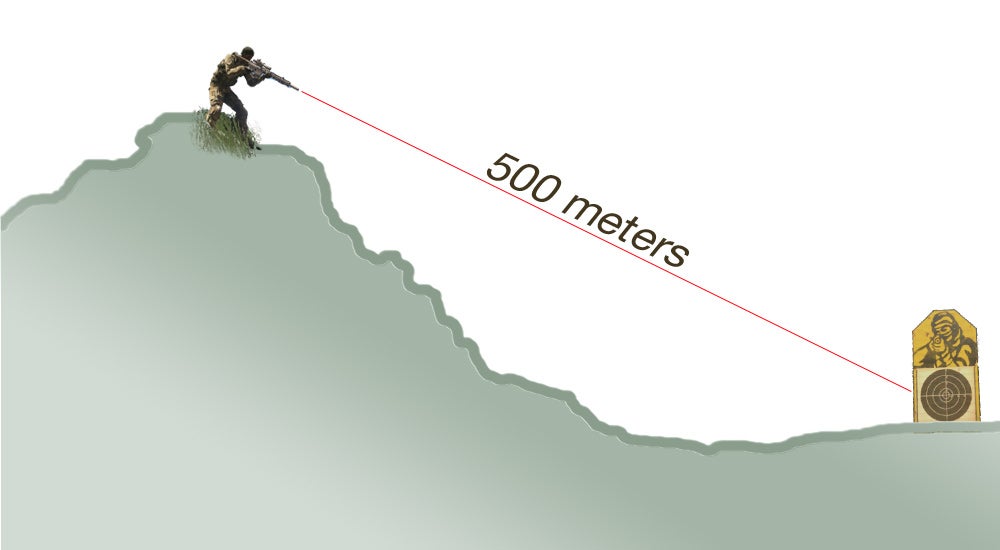
This is somewhat counter intuitive, so lets take a closer look by going step by step through a simplified scenario. Our shooter is up on a cliffside, while our target is down in the bottom of the valley, like so:

Using a basic rangefinder, shooter’s intuition, or god-like omnipotence: we learn the distance between us and our target:

At this point instinct says we should dial our scope for 500 meters, line up our crosshair, and squeeze the trigger. That would result in a miss when the bullet flies over the target.

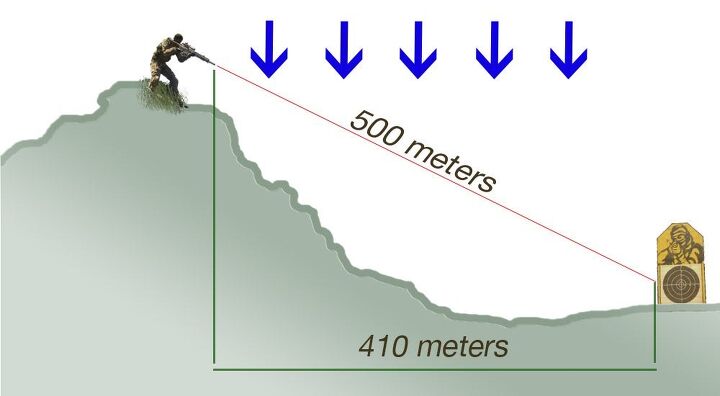
You see, gravity is what causes our bullet to drop. And gravity doesn’t care about that little dip in the ground. Its force doesn’t change with the rock face. It’s always pulling straight down, towards the center of the earth. Like this:

A Note on Physics Abstraction: I realize that on a macro scale Earth’s gravitational pull is spherical, and that on a micro scale gravitational pull exists between all atoms, but for the purposes of this illustration we’re using gravity as the consistent force that pulls things “down.”

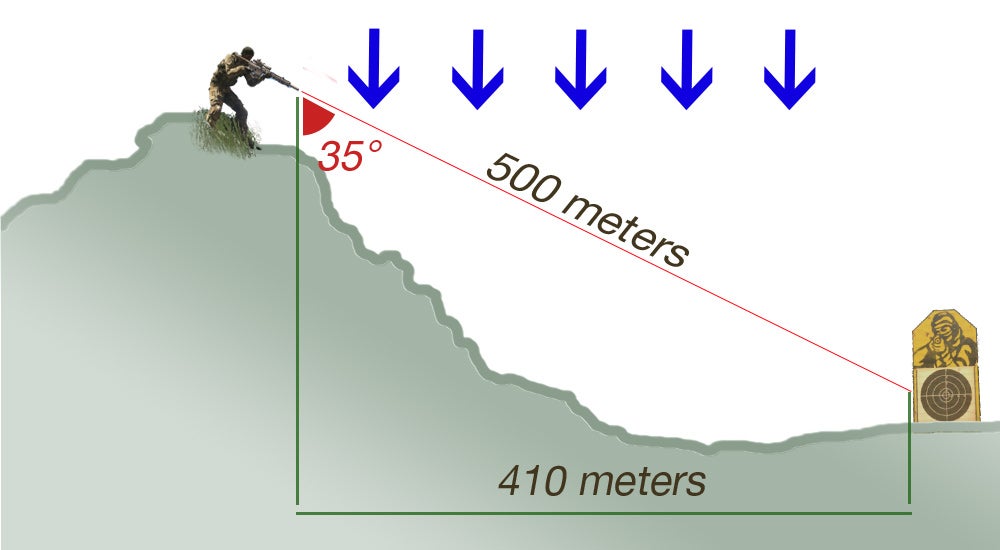
Although the bullet is travelling the full 500 meter path between us and the target, it is only being affected by 410 meters worth of gravity. The drop effect on our bullet is caused by gravity, and at an angle the bullet experiences less of it than when fired horizontally.

When we’re dialing in our scope, we want to be using that 410 meter measurement in our calculations, because that’s how much drop is being applied to the round.

Remember that this works both ways. If the target was to take a shot at our shooter, the bullet would follow the same flight path back up the hill, and experience a similar amount of gravitational drop.

Most modern rangefinders have the ability compensate for this by using an integrated inclinometer. So they will calculate the angle difference when aiming up or down, and display the practical distance to the shooter.

If this is starting to look like basic High School trigonometry to you: Congratulations! That’s exactly what it is. And if you have no memory of High School trigonometry whatsoever, don’t panic. Almost none of us remember that stuff, the point of a good rangefinder is that it will do all that math for you in the field.

If you’re looking for more detailed and technical explanations of what’s happening here, along with all the fun formulas and charts, there’s lots of resources online from great shooters like Bryan Litz and the like. Here’s a quick reading list of similar explanations that go deeper:

Exterior Ballistics: Inclined Fire
Long Range Shooting: Angle Shooting
Wikipedia’s Entry on “the Rifleman’s Rule”