Why do some cartridges burn barrels more than others? What makes a smaller-caliber, higher velocity round toastier to your bore, and how can you compare one caliber to another in this respect? While it’s not the whole answer to this question, today we’re going to talk about a major component to this equation, and that’s heat flux.

Note: For all the engineers out there, the units we’ll be working in are kJ/cm^2, which are not the normal units for heat flux in engineering (those would be Watts/unit area). The reason for this is that for the purposes of a gunshot, the missing unit of time is not important. In other words, we are measuring the energy dumped per gunshot. This is very useful, as we can combine this unit with a rate of fire figure to approximate the actual heat flux (in W/unit area) of a gun over a given course of fire.

Oh, and for those following my math, I am using approximate unit conversion factors of 25.4 mm per inch, 15.43 grains per gram, and 3.28 feet per meter.

It may be easy to tell which of the pair on the left will erode the barrel faster, but it’s much more ambiguous for the pair on the right. Having a way to compare cartridges in this respect is useful.

First, we need a couple of examples to compare. Let’s take the common 5.56x45mm M193 Ball loading, for starters. We know a few relevant things about this cartridge:

– It has a bore diameter of 5.56mm/0.219″, and a groove diameter of 5.69mm/0.224″. Either of these dimensions can be used for calculating heat flux, as long as which one is chosen is kept constant when comparing different calibers. Since groove diameter is the more commonly available figure – it is usually the same as the bullet diameter, we will use it.

– It has uses a charge of approximately 1.72g/26.5grs.

– It produces a muzzle velocity from a 50.8cm/20″ barrel of about 997 m/s or 3,270 ft/s.

– It has a bullet weight of 3.56 grams or 55 grains.

From these figures alone we can calculate heat flux. We should start by calculating the muzzle energy of the round, using the kinetic energy equation KE  = 0.5 * (mass of the bullet) * (muzzle velocity)^2. I prefer doing my calculations in metric, so that would be:

MKE = 0.5 * 3.56 g * (997 m/s)^2 = 1,769 Joules

Next, we need to calculate the total energy produced by the cartridge. This is not the same as the muzzle energy, as guns are not perfectly efficient engines, so to approximate this we need to take the powder charge in grams and find out how much energy it produces when it burns. There’s not an easy way to do this exactly, so instead we’ll take a shortcut by just using a fixed figure of 3,870 Joules produced per gram, which is converted from a figure of 185 ft-lbs per grain estimate for IMR brand powders. This step is where most of the error will be introduced as that figure may not be correct for every kind of propellant (though it shouldn’t be wildly off for nitrocellulose-based propellants), and because for some barrel length-cartridge combinations a lot of unburnt powder may be ejected out the muzzle (and therefore its energy won’t go into heating the barrel). However, for a quick rule-of-thumb estimate, it’s not bad.

For M193, we find:

TKE = 3,870 J/g * 1.72 grams = 6,656 Joules

Giving us a wasted energy figure of:

6,656 Joules – 1,769 Joules = 4,887 Joules

Or 4.887 kilojoules (kJ). Now, find the area of the bore, or in this case the approximated area from the groove diameter:

5.69 mm / 2 = 2.845 mm

π * (2.845 mm)^2 = 25.4 mm^2 = 0.254 cm^2

Now, finally, we can find the heat flux per shot by dividing the approximate wasted heat in kilojoules by the approximate area of the bore in square centimeters!

4.887 kJ / 0.254 cm^2 = 19.2 kJ/cm^2

And that’s the approximate heat flux for a single shot of M193 Ball ammunition, through a 20″ barrel. By calculating values for different calibers, you can compare them to get a better idea of which calibers burn barrels out faster than others.

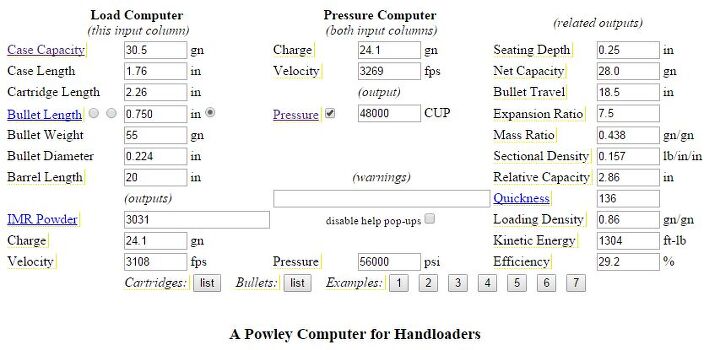
You can also use the excellent Powley computer hosted at kwk.us to do this calculation as well, though it’s not necessary. To do so, fill in all the values for case capacity, case length, cartridge overall length, bullet length, etc, and adjust the pressure to the correct value by clicking the checkbox next to the “Pressure” section. Then use it to find the total kinetic energy value by dividing the muzzle energy by the efficiency (convert the efficiency from percent to decimals first), and pick up the instructions above from there! A screenshot of what a filled in Powley sheet looks like is below: